While working on text rendering for my projects, I developed an algorithm for SDF font atlas calculation on GPU. The algorithm requires OpenGL 2.0 capable hardware and fast enough for generating font atlases at runtime. The demo project is availible here (font atlas generator for my text rendering demo).

The algorithm

The algorithm works with vector objects (shapes) defined with closed contours (paths) consisting of primitive segments (line segments, Bézier curves etc.). The algorithm consists of following steps:

1. Outline rendering. Render each primitive segment of a path with depth test enabled and depth funtion set to LESS. In fragment shader calculate the distance from a fragment to the closest point on a contour, clamp it to max_sdf_distance. Interpolate fragment color and depth values linearly with distance, so the fragments with zero distance from the contour will have color value of 0.5 and depth value of 0.0, and fragments with max_sdf_distance will have color value of 0.0 and depth value of 1.0.

2. Stencil fill. Fill the stencil buffer such way, that fragments which lie inside the shape will have the same stencil value (i.e. 1).

3. Color inversion. Invert the color values (1.0 - v) for each fragment that lies inside the shape and have the aforementioned stencil value.

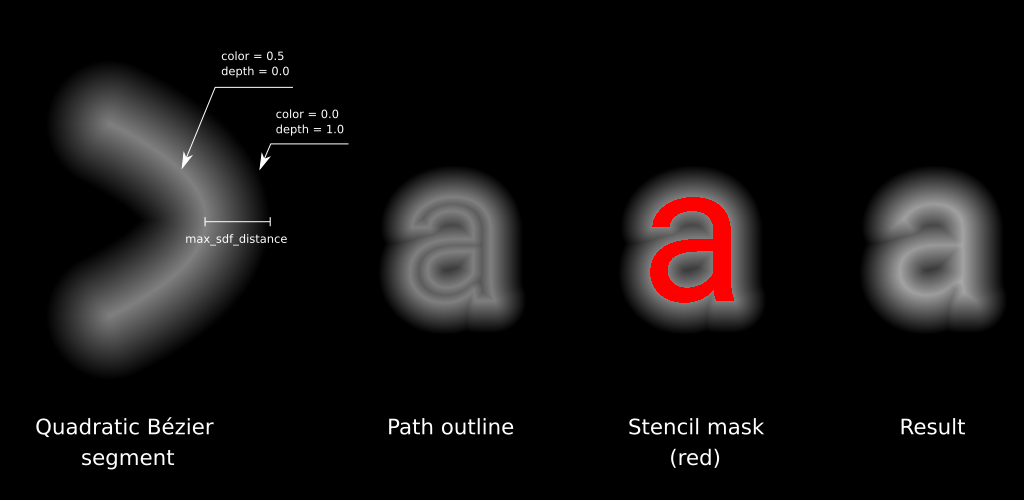
Outline rendering

I’m using this method with TrueType fonts, which use line segment and quadratic Bézier curves as primitives, so I use parabola segment as a primitive inside the fragment shader and calculate the distance from a point to a parabola. I described a method to calculate parameters of a parabola segment, associated with quadratic Bézier in the previous post. For line primitives I also use parabola segments which are strait enough to visualy appear as strait lines.

For each segment a bounding rectangle is calculated and each vertex of the rectangle is transformed to the parabola space. Inisde the shader the cubic equation is solved to calculate the distance from a point to a parabola $y=x^2$. The equation is

$$x^3 + ( \frac{1}{2} - S_y ) x - \frac{1}{2} S_x = 0$$

where $S_x$ and $S_y$ are coordinates of a point in parabola space. The equation is solved almost by the book with few optimizations.

For the points that lie above the evolute of the parabola and have three real roots, heavy cos-acos part

$$2 \cdot \cos \left( \frac {1}{3} \arccos \alpha \right)$$

is approximated with cubic function

$$0.01875324 \cdot \alpha^3 - 0.08179158 \cdot \alpha^2 + 0.33098754 \cdot \alpha + 1.7320508$$

Once the first root is found, the Vietta’s method is used to find the other root (the third root in the middle is never the closest, so it is skipped).

Stencil fill

For the stencil fills I use the method by Kokojima et al. The triangles are formed and rendered so, that front facing triangles increase the stencil value, and back facing ones decrease it.

For each quadratic Bézier segment two triangles are formed. One is always filled, and have one vertex at the starting point of a shape, and two other at the endpoints of a segment. The other triangle have its vertices at the control points of the Bézier. The parabola coordinates vpar are set to [-1,1], [0,-1], [1,1]. The test vpar.x*vpar.x < vpar.y is performed and fragments that passed the test are filled.

The shader works by the method described by Loop and Blinn. I use different values, than Loop and Blinn in their paper. They use [0,0], [0.5,0], [1,1]. The idea behind these magic numbers is pretty simple: pick two arbitrary points on a unit parabola and calculate the intersection point of their tangents to the parabola. Use these coordinates in the shader. This way the triangle vertices act as affine transformation of a unit parabola, which is exactly the way quadratic Bézier works.

Color inversion

The full screen quad is rendered with stencil test enabled and blend function set to GL_ONE_MINUS_DST_COLOR, GL_ZERO.

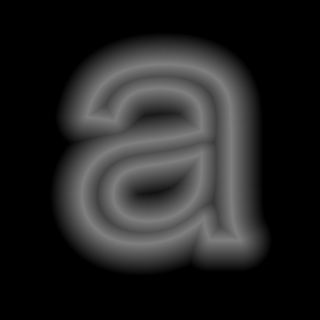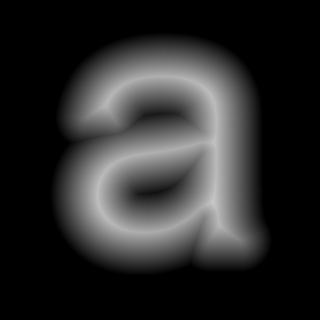
Performance

I use sdf_atlas program with png and JSON saving disabled for benchmarking.

The options are sdf_atlas -f arial.ttf -tw 2048 -th 2048 -rh 96 -bs 16 -ur 0x21:0x7e,0xa0:0xff,0x400:0x4ff.

Number of glyphs rendered: 445, outline triangle count: 18982, fill triangle count: 14551.

Celeron 2955U @ 1.4GHz with Intel HD graphics: font loading and vertex generation 16 ms, atlas rendering 55 ms.

Ryzen 5 1400 @ 3.2GHz with GeForce GTX 1070 : font loading and vertex generation 7 ms, atlas rendering 7 ms.

Comments