Quadratic Bézier Parabola Parameters, Arc Length, and Nearest Point on a Curve

Any non degenerate regular quadratic Bézier is essentialy a affine image of a unit parabola $y=x^2$. An important property of such transformation is that it have orthogonal and uniformly scaled basis. The intuition behind this is that a parabola is defined with a line (directrix) and a point (focus), and no affine transformation can either skew or non-uniformly scale this system. The transformation matrix can be calculated in the following way.

Non-degenerate case

For a quadratic Bézier, defined with control points $A$, $C$, $B$ (see the pic) find a midpoint $M$ of $AB$. The line $CM$ is parallel to the axis of the parabola. Normalizing $\vec{CM}$ we get vector $\vec{Y}$, and rotating it 90° to the right we get vector $\vec{X}$. These vectors with scale applied would form a basis of the transformation.

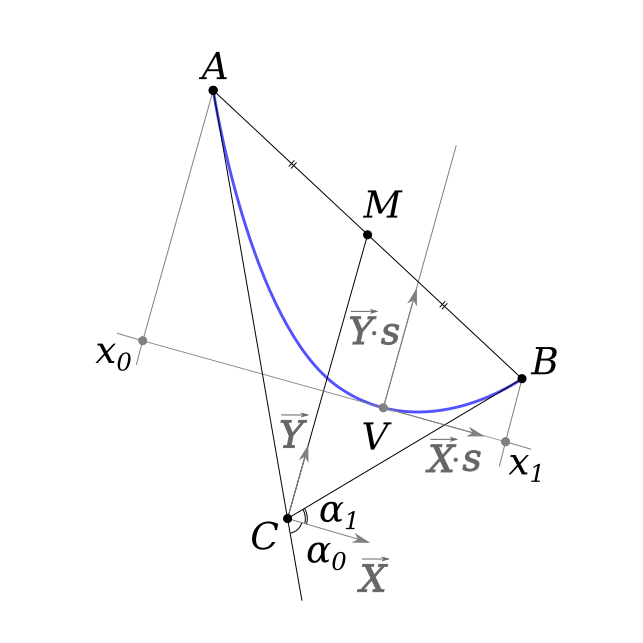
Now to find endpoints $x_0$ and $x_1$ of the parabola segment we should calculate the tangents of angles $\alpha_0$ and $\alpha_1$:

$$\tan\alpha_0 = \frac{\vec{AC} \bullet \vec{Y}}{\vec{AC} \bullet \vec{X}} \quad , \quad \tan\alpha_1 = \frac{\vec{CB} \bullet \vec{Y}}{ \vec{CB} \bullet \vec{X}}$$

Since $AC$ and $CB$ are tangents to the parabola at points $A$ and $B$, considering $(x^2)’ = 2 x$, we get

$$x_0 = \frac{1}{2}\tan\alpha_0 \quad , \quad x_1 = \frac{1}{2}\tan\alpha_1$$

Projecting $\vec{BA}$ to $\vec{X}$ and dividing by distance between $x_0$ and $x_1$, we get the scale of the transformation:

$$s = \frac{\vec{BA} \bullet \vec{X}}{x_1 - x_0}$$

The vertex of the parabola can be found as

$$\vec{V} = \vec{A} - x_0^2 \cdot s \cdot \vec{Y} - x_0 \cdot s \cdot \vec{X}$$

This would give us a translational part, and we can build the transformation matrix:

$$Q = \begin{bmatrix} X_x \cdot s & Y_x \cdot s & V_x \\ X_y \cdot s & Y_y \cdot s & V_y \\ 0 & 0 & 1 \end{bmatrix}$$

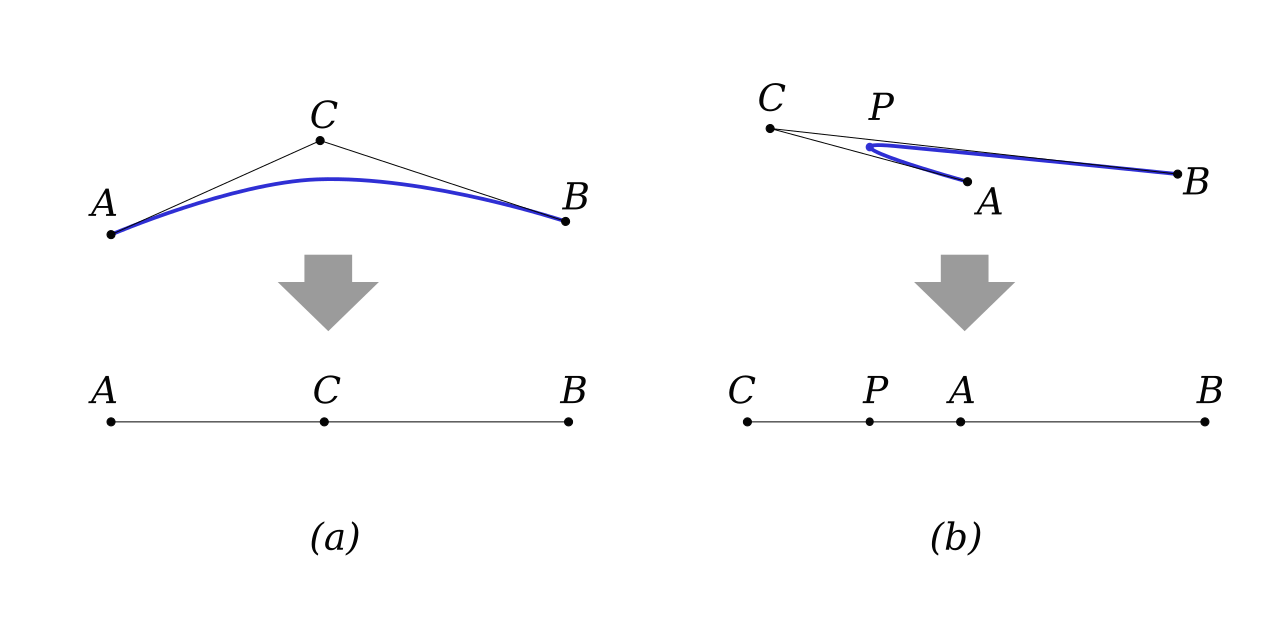
Degenerate cases

In degenerate cases, (a) and (b) on the pic, a quadratic Bézier is either a line segment $AB$ or two line segments $AP$ and $PB$, where

$$P(t) = (1-t)^2 \cdot A + 2 (1-t) \cdot t \cdot C + t^2 \cdot B$$

with

$$t = \frac{\lVert AC \rVert}{ \lVert AC \rVert + \lVert CB \rVert }$$

(in a non-degenerate case the tangent to this point is orthogonal to a bisector of angle $\angle ACB$).

Arc length

In degenerate cases the arc length is the length of the corresponding line segments. In non-degenerate case, the arc length of a quadratic Bézier can be found as

$$l = s \cdot \lvert L(x_1) - L(x_0) \rvert$$

where

$$L(x) = \frac{1}{4} log ( 2 x + \sqrt{ 4 x^2 + 1 } ) + \frac{1}{2} x \sqrt{ 4 x^2 + 1 }$$

Nearest point on a curve

Degenerate cases are trivial. In non-degenerate case, nearest point on a curve to a point $T$ can be found by first transforming $T$ to the parabola coordinate system $S = Q^{-1} T$ and then solving the cubic equation

$$x^3 + ( \frac{1}{2} - S_y ) x - \frac{1}{2} S_x = 0$$

The roots of this equation correspond to the closest points to $S$ on the parabola. Clamp the roots to $[x_0,x_1]$, choose the point nearest to $S$ and transform it back to the world space.

Compass and Straightedge construction

Example of compass and straightedge construction with Geogebra:

https://www.geogebra.org/geometry/caa8bnuh

Comments